AGADIR

Vyhledávání:

osoby
akce
projekty
skladby

Agadir na facebooku:

Agadir na Instagramu:

Agadir na Wikipedii:

Kanál RSS:

Jsme členové
Českého centra Mezinárodního
PEN klubu

Jsme členové
Sdružení Q

Pořady z cyklu
"Agadir: Na strunách naděje"
jsou konány
za finanční podpory
Státního fondu kultury
České republiky

Mediální partneři:

Přihlášený uživatel:
žádný

Vaše IP adresa:
3.141.29.162

Přístupy celkem: 46616779
Přístupy dnes: 3782

Optimalizováno pro rozlišení:
1280x720 a vyšší

Ladění

Stupnice

Hlasové rozsahy

Rozsahy hudebních nástrojů

LADĚNÍ

Ladění (temperatura) stanovuje přesné vzdálenosti jednotlivých tónů v hudební stupnici. Ladění tak určuje frekvence jednotlivých tónů a poměry mezi nimi.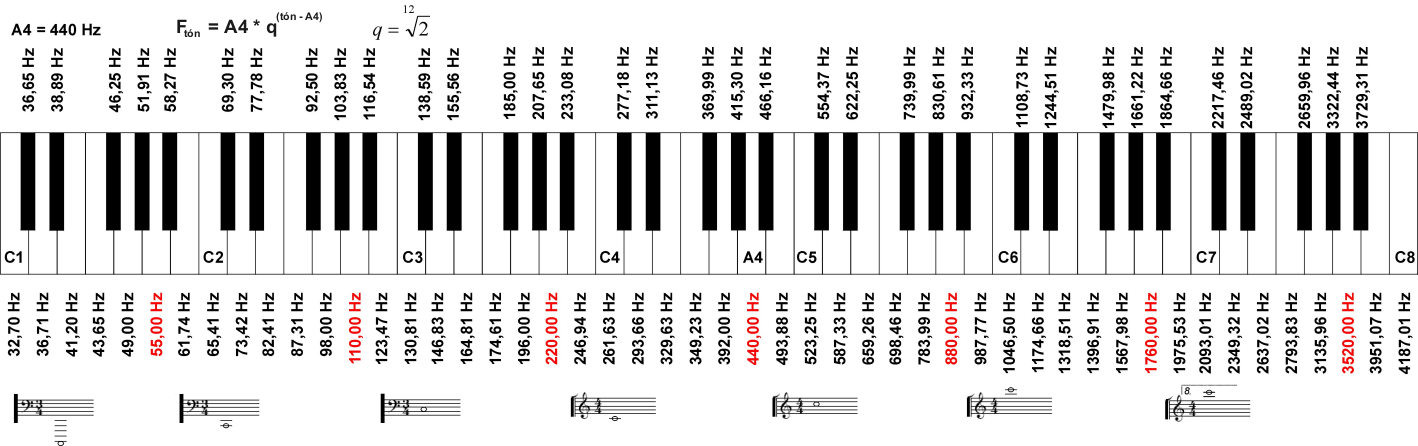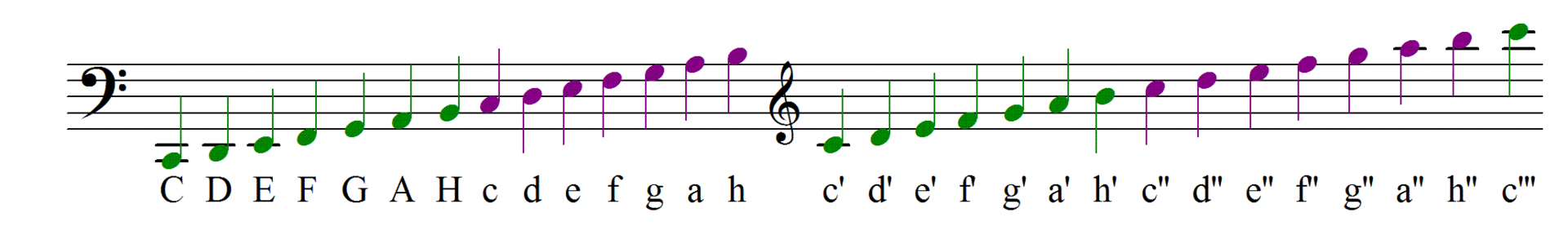

Určení délky skladby podle tempa a metra: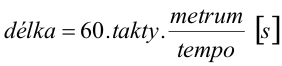

60 ·

Tón a jeho charakteristika

Každý zvuk vzniká chvěním nějakého tělesa. Tělesa kmitající pravidelně, s určitou frekvencí, vydávají tóny (například chvějící se struna); nepravidelně kmitající tělesa, jejichž kmity nemají konstantní frekvenci, vydávají hluky či šramoty (například činely). Základní charakteristiky tónu jsou výška, barva, délka a síla. Pro teorii ladění je důležitá pouze výška tónů, ačkoliv s laděním hluboce souvisí i barva tónu, jak bude objasněno dále.

Vnímaná výška tónu je závislá především na frekvenci kmitání tělesa. Čím vyšší je počet kmitů za sekundu (frekvence), tím vyšší tón vnímáme.

Podstata barvy tónu byla objevena až na přelomu 17. a 18. století. V té době bylo zjištěno, že každý tón obsahuje i celou řadu tónů dalších, které již jako samostatné tóny neslyšíme. Tyto tzv. alikvotní tóny (též tzv. vyšší harmonické frekvence) vnikají tak, že předmět vydávající zvuk se chvěje velmi složitým způsobem, v němž se kromě chvění vcelku zároveň odráží i chvění stále menších a menších částí tělesa. Struna se tedy chvěje celá, zároveň se však chvějí i její poloviny, třetiny apod., teoreticky až do nekonečna. Všechny tyto části struny tedy vydávají své vlastní, sluchem samostatně takřka nezachytitelné tóny. Součtem těchto vlnění vzniká složité vlnění struny, jehož časový průběh a tím i výsledná barva tónu závisí na tom, jak jsou jednotlivé alikvotní tóny silné. Tento princip se neomezuje pouze na struny, velmi podobně se chovají i u trubice dechových nástrojů, lidské hlasivky apod.

Uspořádání alikvotních tónů je naprosto zásadní pro teorii ladění. Základní principy lze ukázat pomocí metody dělení struny. Jak již bylo řečeno, alikvotní tóny vznikají samostatným chvěním poloviny, třetiny a dalších zlomků struny nebo jiného tělesa vydávajícího tón. Není tedy nic lehčího, než zkrátit strunu na příslušný zlomek a zjistit, jaký tón takto zkrácená struna vydává. Struna zkrácená na polovinu zní o oktávu výše než celá; struna zkrácená na třetinu zní o oktávu a kvintu (duodecimu) výše; struna zkrácená na čtvrtinu zní o dvě oktávy výše a tak dále.

Intervaly

Již tedy víme, že vzdálenost mezi první a druhou harmonickou složkou (čili mezi základním tónem a prvním alikvotním) je oktáva. Tento interval je natolik konsonantní, že tóny vzdálené jednu nebo více oktáv označujeme stejným názvem, např. C. Míra konsonantnosti intervalu se dá určit také ze součtu čísel, která se vyskytují v čitateli a jmenovateli zlomku, vyjadřujícího poměr frekvencí tónů intervalu. Po unisonu s poměrem frekvencí 1:1 (součet 2) je další nejjednodušší možný poměr právě u oktávy - 2:1 (součet 3).

Vzdálenost mezi druhou a třetí harmonickou složkou je kvinta; poměr frekvencí je 3:2. Vzdálenost mezi třetí a čtvrtou složkou je kvarta s poměrem frekvencí 4:3, mezi čtvrtou a pátou složkou velká tercie s poměrem frekvencí 5:4 atd. V evropské i jiné hudbě se využívají i intervaly i s jinými poměry, např. velká sexta s poměrem frekvencí 5:3.

Pro teorii ladění jsou důležité především intervaly v rozsahu jedné oktávy, tedy od poměru 1:1 (dva stejné tóny - unisono - čistá prima) do poměru 2:1 (čistá oktáva). Například decima s podílem frekvencí 5:2 lze rozepsat jako oktáva + velká tercie (5:2 = 2:1 x 5:4). Po oktávové transpozici lze tedy z intervalu velké decimy odvodit velikost velké tercie.

Hudební stupnice a určování tónů

Hudební stupnice dává intervalům určitý řád; aby vznikla stupnice, je třeba vyplnit oktávu řadou tónů, což se dělo v průběhu dob značně rozmanitými způsoby.

K nejstarším stupnicím patří pětitónová stupnice bez půltónů, tzv. anhemitonická pentatonika, používaná již ve starověké Číně, Japonsku, Indii a dalších zemích. V pythagorejském ladění je odvozena ze čtyř po sobě následujících kvint: např. c-g-d-a-e; po uspořádání do rozmezí jedné oktávy c-d-e-g-a, na konci doplněná o tón c. Pentatonika se dochovala u některých národů až do dnešní doby.

Základem řeckých stupnic jsou tzv. tetrachordy (posloupnosti čtyř tónů). Rozdělením tercií okolo 5. století př. Kr. vznikly tetrachordy složené pouze z celých tónů a půltónů; kombinací dvou tetrachordů byl položen základ středověkých stupnic - církevních modů. Evropská hudba dospěla ve vývoji až ke dvanáctitónové chromatické stupnici, složené z půltónů.

Vytvořit tuto stupnici tak, aby všechny intervaly byly "čisté" však není možné. Již víme, že oktáva má poměr frekvencí 2:1 = 2. Kdybychom chtěli sestavit stupnici např. z dvanácti čistých půltónů s poměrem frekvencí 16:15, dvanáctý půltón nebude souhlasit s čistou oktávou: (16:15)12 = 2.17. Podobná situace nastává i u dalších intervalů. Nemožnost čistého rozdělení oktávy se snaží každý systém ladění obejít způsobem, který je co možná nejpříjemnější pro poslech; každý však musí v něčem ustoupit. Například v pythagorejském ladění existuje tzv. Pythagorejské komma, ve všech "barokních" laděních zní stupnice v tóninách vzdálených od základní tóniny falešně apod.; více informací lze najít u jednotlivých ladění. V současnosti používané rovnoměrně temperované ladění sice rozděluje oktávu na dvanáct stejných půltónových intervalů s poměrem frekvencí, žádný interval kromě oktávy však nemá "přirozenou" velikost, vyskytující se v alikvotních tónech.

Čistá ladění

Jako čistá nebo také přirozená ladění se označují ladění využívající pouze tóny, jejichž frekvence jsou ve vzájemných poměrech vyjádřitelných celými čísly. Přesné významy těchto termínů jsou však poměrně nejednotné. Do této skupiny mimo jiné patří:

Pythagorejské ladění - pro odvození všech tónů používá oktávu 2:1 a kvintu 3:2.

Didymické čisté ladění přidává ještě interval velké tercie 5:4.

Ladění s intervaly obsahujícími prvočísla větší než 5 se v tradiční evropské hudbě nepoužívají.

V případě použití čistých laděních mají intervaly "přirozenou" velikost, danou poměrem celých čísel. Pokud jsou tato čísla dostatečně malá, znějí souzvuky "čistě" a přinášejí velice příjemný sluchový vjem. Tato ladění mají ale i své nevýhody, které fakticky znemožňují jejich použití v běžné současné evropské hudbě. Důsledné uplatnění čistých ladění by vedlo k nekonečně velkému počtu tónů v oktávě. Při použití omezeného počtu tónů se v systému ladění objevují "nečisté", nelibozvučné intervaly (označují se jako tzv. vlčí intervaly). Přesné frekvence jednotlivých tónů se navíc v různých stupnicích u čistých ladění liší, (nota A v C dur nemá stejnou frekvenci jako nota A v D dur). Při modulaci do jiné tóniny znějí proto některé intervaly rozladěně, čistá ladění jsou tedy pro složitější hudbu, využívající modulací, prakticky nevyužitelná. V čistých laděních také není možná enharmonická záměna většiny tónů (například C# není Db). Toto působí potíže při konstrukci a ladění nástrojů s pevnými výškami tónů.

Temperovaná ladění

Pro zmírnění některých výše uvedených problémů čistých ladění bylo vytvořeno mnoho temperovaných ladění, u nichž jsou některé čisté intervaly záměrně rozladěny, aby se docílilo přesnějšího naladění intervalů jiných. Nejvýznamnější předností temperovaných ladění je umožnění modulace i do jiných tónin, aniž by se v nich objevovaly disharmonické vlčí intervaly. U většiny těchto ladění také existuje enharmonická záměna (například D# = Eb = Fbb...), která umožňuje omezit počet tónů v oktávě (v evropské hudbě na 12). Tato ladění se dají rozdělit do dvou skupin:

Nerovnoměrně temperovaná ladění

Rovnoměrně temperovaná ladění

Nerovnoměrně temperovaná ladění

Nerovnoměrně temperovaná ladění mají frekvence tónů upraveny tak, aby blízké tóniny od základní tóniny zněly co nejlépe a vzdálené tóniny alespoň použitelně. Některé intervaly jsou "preferované" - jsou temperované tak, aby vycházely jako čisté; některé zní disonantněji. Do této skupiny patří celá řada ladění, mimo jiné

Parejovo ladění (1482)

Schlickovo ladění (1511)

Grammateovo ladění (1518)

Středotónové ladění (nejrozšířenější ladění 16.-17. století)

Werckmeisterovo ladění (1691)

Kirnbergerovo ladění (1766,1771,1779)

Walottiho ladění

Youngovo ladění

Rovnoměrně temperované ladění

Rovnoměrně temperované ladění je v současnosti nejpoužívanějším laděním v evropské hudbě. Všechny intervaly stejného druhu (kvinty, kvarty, tercie atd.) jsou stejně velké (stejně "rozladěné"), ale žádný interval kromě oktáv není úplně "čistý". Také všechny tóniny jsou rovnocenné, modulace je možná do libovolně vzdálených tónin bez vlivu na zvukovou kvalitu intervalů.

Rovnoměrně temperované ladění vznikne z pythagorejského ladění s 12 stupni v oktávě temperováním (zmenšením) všech čistých kvint o přibližně 1,96 centů. Rovnoměrně temperované ladění je také 1/11-koma středotónovým laděním. K témuž ladění lze dospět také rozdělením oktávy na dvanáct stejně velkých intervalů, toto ladění proto bývá označováno také jako 12edo (equal division of the octave).

Na rozdíl od ostatních ladění je u rovnoměrně temperovaného ladění vzdálenost (poměr kmitočtů) mezi jakýmikoli dvěmi sousedními půltóny totožná. Přesně stejné jsou i všechny intervaly stejného druhu (kvinty, kvarty, tercie atd.).

Zavedení temperovaného ladění bylo výsledkem hledání ladění, vhodného pro potřeby modulace do vzdálených tónin. Jeho všeobecnému zavedení v evropské hudbě předcházelo mnoho nerovnoměrně temperovaných ladění, z nichž některá se používají dosud, zvláště při ladění varhan.

V pythagorejském ladění získáváme všechny intervaly postupnými kvintovými kroky. Po dvanácti krocích je mezi krajními tóny malý interval, nazvaný pythagorejské koma, jehož velikost je je asi 23,46 centů, tedy necelá čtvrtina půltónu. Pokud rozdíl mezi těmito tóny zanedbáme a provedeme enharmonickou záměnu, získáme chromatickou stupnici s 12 tóny v oktávě. V této stupnici jsou všechny kvinty čisté (3:2, 701,96 centů) pouze kvinta mezi krajními tóny je o Pythagorejské koma menší (678,5 centů) a zní velmi rozladěně. Zmenšením čistých kvint o malé intervaly (temperováním) se zbývající kvina zvýší o součet těchto intervalů. Je-li velikost všech malých "korekčních" intervalů shodná, nazývá se vytvořené ladění středotónovým, je-li různá, jedná se o nerovnoměrně temperované ladění. Pokud všech 11 čistých kvint zmenšíme o 1/12 pythagorejského komatu, bude mít zbývající kvinta stejnou velikost jako ostatní kvinty, ptyhagorejské koma bude tedy rovnoměrně rozděleno mezi všech 12 kvint. Vytvořené ladění se proto nazývá rovnoměrně temperované.

Jelikož 1/12 pythagorejského komatu je přibližně přibližně 1/11 syntonického komatu, je rovnoměrně temperované ladění zároveň 1/11-koma středotónovým laděním.

K ladění se stejnou strukturou můžeme dospět také přímo rozdělením oktávy na 12 stejně velkých intervalů. Interval oktávy je vyjádřen poměrem frekvencí dvou tónů 2:1 (zdvojnásobíme-li frekvenci jakéhokoli tónu, dostaneme tón o oktávu vyšší). Je-li třeba rozdělit oktávu na dvanáct stejných dílů (půltónů), musíme dvanácti kroky dosáhnout dvojnásobku výchozí frekvence.

Exotická ladění

Tradiční indické ladění dělí oktávu na 22 dílů (šruti), dnes však základních sedm stupňů mnohdy odpovídá evropské diatonice. Některá arabská ladění vycházejí z ladění pythagorejského, oktávu však dělí na 17 stupňů. V moderní teorii arabské hudby se často používá dělení oktávy na 24 shodných dílů - temperovaných čtvrttónů.

V hudbě mnoha kultur není harmonie a konsonance podstatným prvkem v hudbě. Používané hudební nástroje bývají proto laděny zcela odlišným způsobem, který obvykle není založen na matematických principech. Např. indonéské systémy sléndro a pélog nepoužívají čisté oktávy a přesné výšky tónů se u jednotlivých nástrojů a orchestrů liší. Podobná je i situace u mnoha ladění, používaných v africe.

Další typy ladění

Kromě ladění, která je možné označit za tradiční, existuje velké množství ladění dalších, která jsou používána v mikrotonální hudbě. Mnohá mají za základ čistou oktávu, dělí ji však na jiný počet dílů než je obvyklé. K nejznámějším patří ladění čtvrttónové, bežné je i dělení na 19, 22, 53 nebo 72 dílu. Některá ladění nemají za základ oktávu, ale jiný interval. K nim patří ladění Bohlen-Pierce vycházející z duodecimy 3:1, nebo stupnice alfa, beta nebo gama, které vytvořila Wendy Carlos. Lze vytvořit i ladění, jejichž struktura se po žádné transpozici neopakuje.

Pythagorejské ladění

V pythagorejském ladění jsou všechny tóny oktávy získány postupnými kvintovými kroky.

Má-li základní tón relativní frekvenci 1, má o kvintu vyšší tón frekvenci 3:2. Tón o další kvintu vyšší má frekvenci (3:2)×(3:2)=9:4. Tón o kvintu nižší než základní tón má frekvenci 2:3, tón o další kvintu nižší má frekvenci (2:3)×(2:3)=4:9. Dvěma kvintovými kroky nahoru a dolu získáme tedy 5 tónu s frekvencemi 4:9, 2:3, 1:1, 3:2 a 9:4.

Tón 9:4 leží výše než oktáva k základnímu tónu (9:4 je větší než 2:1). Snížíme ho proto o oktávu (frekvenci vydělíme dvěma) a získáme tón s frekvencí 9:8. Podobně o jednu oktávu zvýšíme tón 2:3, ležící pod základním tónem, a dostaneme tón s frekvencí 4:3. Nejnižší tón zvýšíme o dvě oktávy a získáme tón 16:9. Nová řada v rozsahu oktávy tvoří pětitónovou stupnici - pentatoniku: 1:1, 9:8, 4:3, 3:2 a 16:9.

V oktávě máme tyto intervaly:

Relativní frekvence	Interval
1	prima
9:8	velká sekunda
4:3	čistá kvarta
3:2	čistá kvinta
16:9	malá septima
2:1	oktáva

Mezi sousedními tóny jsou intervaly 9:8 (velká sekunda) nebo 32:27 (malá tercie).

Dalším kvintovým krokem nahoru a dolů a přemístěním nových tónů do základní oktávy vytvoříme diatonickou stupnici, tvořenou sedmi tóny: 1:1, 9:8, 32:27, 4:3, 3:2, 27:16, a 16:9.

Didymické čisté ladění

Didymické ladění je nejběžnější z čistých hudebních ladění. Mnohdy bývá pojmem čisté ladění označováno právě ladění Didymické.

Toto ladění zní absolutně čistě v tónině odvozené od základního tónu, již ve velmi příbuzných tóninách se ale začínají vyskytovat velice disonantní vlčí intervaly, takže čisté ladění je pro složitější hudbu prakticky nepoužitelné. Příkladem může být vlčí kvinta D-A: (5:3) x (8:9) = 40:27, čili asi 1,4815; čistá kvinta je 3:2 = 1,5.

Základ ladění vytvořil v prvním století hudební teoretik Didymus z Alexandrie, který vyšel z dělení struny v poměru 24:27:30:32.

K oktávě 2:1 a kvintě 3:2, které byly použity již při konstrukci pythagorejského ladění, byly přidány intervaly, v nichž se objevuje číslo 5. Disonantní Pythagorejská velká tercie 81:64 byla nahrazena Didymickou velkou tercíí 5:4 a Pythagorejská velká sexta 27:16 Didymickou sextou 5:3. Rozdíl mezi Pythagorejskou a Didymickou tercií nebo Pythagorejskou a Didymickou sextou se nazývá Didymické koma.

Parejovo ladění

Parejovo ladění je nerovnoměrně temperované ladění, které ve svém traktátu popsal španělský hudební teoretik Bartolomeo Ramos de Pareja (datováno 1482).

Vyšel, jak bylo v té době obvyklé, z ladění pythagorejského. Ladil trudíž podle čistých kvint, přitom ale na jednom místě naladil čistě velkou tercii F-A. Tím pádem mu namísto pythagoreského komatu vzniklo koma syntonické a to nevytlačil až na kraj tónové řady, jak bylo běžné, ale nechal jím zmenšit jim přímo kvintu G-D. Tím pádem získal několik po sobě jdoucích čistě naladěných kvintakordů: B-dur, F-dur, C-Dur, d-moll, a-moll, e-moll. Vypadá to, že i když vycházel z ladění pythagorejského, tedy kvintového, předznamenal svým postupem ladění středotónové, založené na vylepšení tercií.

Postup byl tedy následující: Od tónu F naladil čistě spodní velkou tercií tón F. Potom od tónu F postupoval kvintovým kruhem (tedy pythagorejsky) na tóny C, G, D a potom z tónu A spodní kvintou na D. Tím pádem vznikla kvinta G-D, zúřená oproti čisté o velikost syntonického kommatu. Zbývající tóny naladil opět po čistých kvintách: od tónu A po směru kvintového kruhu naladil postupně E, H, Fis a Cis a od tónu F proti směru kvintového kruhu tóny B, Dis, Gis. Tím pádem mu mezi tóny Cis a Gis vznikla kvinta, užší oproti čisté pouze o schisma (1,9 centu, což je hodnota velice blízká jedné dvanáctině pythagorejského komatu, tj. tato kvinta byla naladěná prakticky rovnoměrně temperovaně).

Schlickovo ladění

Schlickovo ladění je nerovnoměrně temperované ladění, které ve své práci v roce 1511 popsal Arnolt Schlick. Zatímco někteří hudební teoretici kladou Schlickovo cítění ještě do doby temperatur, odvozených z pythagorejského ladění, založeného na kvintách, jiní již v této práci hledají začátky vzniku středotónového ladění, založeného na velkých terciích.

Arnold Schlick svůj návod k ladění varhan popisuje zhruba následujícími slovy: "Začni s tónem F v manuálu a vem jeho horní kvintu a neber ji příliš vysoko (jak by odpovídalo čistému ladění), ale nech ji podle záznějů o něco níže, co sluch ještě snese, ale zase ne až tak moc...". Z tohoto popisu lze stěží odvodit exaktní vztahy mezi tóny, které požaduje přesná hudební teorie, pracující s pojmy pythagorejské či syntonické koma a poměřující drobné odchylky intervalů na centy, a proto jsou pokusy o rekonstrukci Schlickova ladění nejisté.

J. Murray Barbour se jako první pokusil o rekonstrukci Schlickova ladění, přičemž vycházel z jedné šestiny pythagorejského komatu (PK). Kvinty F-C, C-G, G-D, D-A, A-E, E-H jsou laděny o 1/6 PK níže než čistě (698 centů), kvinty H-Fis, Fis-Cis, Dis-B a B-F jsou laděny o 1/12 PK níže než čistě, tzn. prakticky se rovnají kvintám rovnoměrně temperovaného ladění, jak je známe dodnes (700 centů), a Kvinty Cis-Gis a Gis-Dis jsou laděny o 1/6 PK výše než čistě (706 centů).

Helmut K. H. Lange pokládá Barbousovu rekonstrukci za mylnou a naproti tomu se domnívá, že bylo Schlickovo myšlení již pevně svázáno se středotónovým laděním. Proto zužuje ladění oněch šesti kvint o 3/16 syntonického komatu.

Wegscheider s Wernerem naproti tomu dávájí za pravdu Barbourovi a ukazují, že je to naopak Lange, který vychází ze špatného předpokladu o Schlickově svázanosti se středotónovým laděním. Tvrdí, že z pozorného čtení Schlickova díla jasně vysvítá, že jeho myšlení ještě navazuje na Pythagorejské ladění, a proto se znaží zachovat konsonanci kvint do té míry, pokud je to možné. Odvolávají se na myšlení té doby, zejména na ladění Pereji (1428, tj. pouze 29 let před Schlickem) a Grammatea (1518 - ještě téměř 7 let po Schlickovi), jejichž ladění rovněž vychází z pythagorejského.

Grammateovo ladění

Grammateovo ladění je nerovnoměrně temperované ladění, které ve své knize v roce 1518 popsal Heinrich Schreyber alias Henricius Grammateus z Erfurtu.

Diatonické tóny stupnice C-dur ladí čistě pythagorejsky. Pro naladění půltónů pak volí geometrický střed mezi sousedními tóny (tj. např. tón Cis posazuje mezi sousední diatonické tóny C a D). Tím pádem dělí pythagorejské koma na dvě poloviny.

Středotónové ladění

Středotónové ladění je nerovnoměrně temperované hudební ladění vynalezené v průběhu 16. století a používané především v dobách raného baroka. Nejčastěji je tímto termínem označováno 1/4-koma středotónové ladění, o kterém se v roce 1511 poprvé zmínil Arnold Schlick a které podrobně popsal Pietro Aron v roce 1523.

Až do vrcholného středověku se za konsonantní intervaly považovaly jen oktáva, kvinta a kvarta; až postupem času se k nim začaly řadit i tercie a sexta. Starověké Pythagorejské ladění odráží tento dobový úzus - preferuje čisté kvinty a kvarty na úkor tercií a sext, které v tomto ladění znějí v souzvucích disonantně.

S potřebou konsonantních čistých (Didymických) tercií s poměrem frekvencí 5:4 se objevila temperovaná ladění, k nimž patří i ladění středotónová. Temperováním (mírným zmenšením) každé kvinty dojde také ke zmenšení příliš širokých pythagorejských velkých tercií 81:64 (407,82 centů) a jejich přiblížení k požadovaným čistým terciím 5:4 (386,31 c). Jelikož interval (rozdíl) mezi Pythagorejskou a Didymickou velkou tercií je označován jako syntonické koma (81:80, 21,51 c), je míra temperatury (míra zmenšení kvinty) obvykle vyjadřována zlomkem syntonického komatu.

Temperovaných kvint je 11, zbylá dvanáctá kvinta z kvintového okruhu má odlišnou "zbývající" velikost. Ve středotónových laděních s velkými terciemi, blízkými čistým terciím 5:4, je tato poslední kvinta velice disonantní a v hudbě nepoužitelná, proto se označuje jako tzv. vlčí kvinta.

Nejběžnější středotónové ladění temperuje každou z jedenácti kvint o čtvrtinu syntonického komatu. Syntonické koma je 81:80, čtvrtina z něj činí (81:80)1/4 (v hudbě se pracuje s geometrickými, nikoliv aritmetickými řadami). Kvinta 3:2 zmenšená o (81:80)^1/4 je (3:2)/(81:80)^1/4 = 1,495 (696,58 c). Kvinty jsou tedy o 5,38 centů užší než kvinty čisté (701,96 c), velké tercie vycházejí jako čisté.

Werckmeisterovo ladění

Werckmeister je nerovnoměrně temperované ladění, které na konci 17. století vytvořil německý hudební teoretik Andreas Werckmeister. Toto ladění bylo ve své době občas používáno jako náhrada tehdy převládajícího středotónového ladění. Na rozdíl od něj je ve Werckmeister ladění kvintový kruh uzavřen, nevyskytují se zde proto žádné vlčí intervaly a tím je umožněna hra i ve vzdálených tóninách od základního tónu. Na rozdíl od středotónového ladění, které temperuje syntonické koma, Werckmeister temperuje pythagorejské koma (stejně jako dnes používané rovnoměrně temperované ladění).

Andreas Werckmeister sestavil celkem čtyři typy ladění, která zveřejnil ve svém díle "Musikalische Temperatur" (1691). Zde popsal i čisté ladění (pod číslem I) a středotónové ladění (pod číslem II), svá čtyři ladění označil čísly III - VI. V literatuře se používá buď původní označení "Werckmeister III - VI", nebo "Werckmeister I - IV". Werckmeister III (původní označení) je nejznámější a jediné, které bylo často používáno. Když se nějaké ladění označuje jako "Werckmeister" (bez udání čísla), zpravidla se tím myslí právě toto ladění.

Kirnbergerovo ladění

Kirnberger je nerovnoměrně temperované ladění, které na konci 18. století zkonstruoval německý hudební teoretik a skladatel Johann Philipp Kirnberger.

V Kirnbergerově době se používalo mnoho různých druhů ladění: středotónové (takto byly laděny zvláště varhany), velký počet různých druhů nerovnoměrně temperovaných ladění a prosazovat se začalo i rovnoměrně temperované ladění. V porovnání s ostatními nerovnoměrnými temperaturami se Kirnbergerovo ladění vyznačovalo relativně jednoduchou stavbou a silnou orientací na čisté intervaly. Kirnberger vytvořil tři typy ladění, dnes označovaná jako Kirnberger I (r. 1766), II (r. 1771) a III (r. 1779).

Kirnberger I: V tomto ladění jsou čtyři velké tercie čisté, ostatní tercie ale zní velmi disotantně a jsou přítomné i čtyři příliš široké pythagorejské velké tercie. Také kvinta D - A zní velice disonantně.

Kirnberger II: V tomto ladění již zní kvinta D - A přijatelněji, ale na úkor snížení počtu čistých velkých tercií na tři. Pythagorejské velké tercie zůstávají čtyři, hodnoty ostatních velkých tercií se v porovnání s Kirnberger I přiblížily čistým velkým terciím.

Kirnberger III: Všechny kvinty již znějí přijatelně, zůstala ale jen jedna čistá velká tercie, počet pythagorejských velkých tercií se omezil na dvě.

Zdroj: Encyklopedie WIKIPEDIA